Problemstellung:
Bestimmung der optimalen Losgröße

Die Berechnung der optimalen Losgröße ist eine typische betriebswirtschaftliche Aufgabenstellung aus dem Bereich der Produktion. Dabei geht es darum, welche Stückzahlen produziert werden, bevor die Anlage für die Produktion eines anderen Produktes umgerüstet wird.

Optimale Losgröße Definition

Die Problemstellung der optimalen Losgröße – was ist die kostengünstigste Losgröße: 100 Stück, 200 Stück … 1.000 Stück? – ähnelt der Fragestellung der optimalen Bestellmenge. Es gibt wiederum 2 Aspekte bzgl. der Kosten zu berücksichtigen:

• produziert das Unternehmen kleine Losgrößen (im Extremfall: 1 Stück), sind die Lager und damit die Lagerhaltungskosten (Kapitalbindung, Lagermiete, Lagerpersonalkosten) klein, dafür aber die sog. auflagenfixen Kosten (Rüstkosten) hoch (die Maschinen müssen nach jedem Los umgestellt werden);
• werden hingegen große Lose hergestellt, sind die Lagerhaltungskosten höher, dafür aber die auflagenfixen Kosten geringer.

Die Formel für die optimale Losgröße (auch als Andlersche Formel bezeichnet) löst diesen Zielkonflikt wiederum analog zur Vorgehensweise bei der optimalen Bestellmenge:
https://welt-der-bwl.de/Optimale-Losgröße

Aufgaben

Klasse: Lege eine Klasse mit dem Namen Produktion an. Sie hat folgende Instanzvariablen. Wähle geeignete Datentypen.

• Produktname
• Herstellkosten
• Jahresproduktion
• Rüstkosten
• Lagerhaltungskostensatz

Programmiere folgende Methoden:

1. Konstruktor
2. ProduktinformationenDrucken
   Hier wird lediglich Informationen zum Produkt auf dem Bildschirm ausgegeben. Überlege Dir dazu einen geeigneten Satz bzw. Sätze.
3. wurzelziehen (und Runden)
   Da wir ja Wurzelziehen und runden häufiger brauchen, sollte dafür eine Methode erstellt werden. Übergabeparameter sind Wert aus dem die Wurzel gezogen wird.  Wir runden zudem auf 0 Nachkommastellen. Rückgabeparameter ist ein Double-Wert.
   Wurzel ziehen: In der Mathematik ist die zweite Wurzel (Quadratwurzel) einer Zahl identisch mit der Zahl hoch 0,5. Somit kann die Methode math.pow(wert,0.5) verwendet werden.
4. Optimale Anzahl der Lose berechnen
   Formel: = Wurzel aus (Lagerhaltungskostensatz * Jahresproduktion*0.5*Herstellkosten / Rüstkosten); Kein Übergabeparameter; Rückgabe: Optimale Anzahl Lose (als Double); Diese Methode ist private.
5. Optimale Anzahl der Lose drucken
   Die errechnete Anzahl Lose wird ausgedruckt.
6. Optimale Losgroeße berechnen
   Errechnet sich aus Jahresproduktion / Optimale Anzahl Lose
   Zudem soll das Ergebnis ausgedruckt werden.
7. GesamtkostenBerechnen (in Abhängigkeit der Lose)
   Import sind die Lose (=Wie oft im Jahr umgerüstet wird)
   Berechnet werden folgende Dinge:
   • Losgröße (=Jahresproduktion / Lose)
   • Rüstkosten pro Jahr (Rüstkosten * Lose)
   • Durchschnittlicher Lagerbestand (= Losgröße / 2)
   • Lagerbestandswert (=Durchschnittlicher Lagerbestand * Preis pro Stück)
   • Lagerkosten (=Durchschnittlicher Lagerbestandswert * Lagerkostenzinssatz)
   • Gesamtkosten (Lagerkosten + Rüstkosten)

Runde Eurobeträge auf 2 Nachkommastellen und Mengen auf 0 Nachkommastellen. Diese Informationen sollen auf den Bildschirm gedruckt werden. Zurückgegeben (return) werden nur die Gesamtkosten. Diese Methode ist private.

7. KostenAusgeben (1)
   Import ist die maximale zu berücksichtigende Anzahl der Lose die ausgegeben wird.  Anfangen bei  1 wird für jede weitere Anzahl eine Zeile ausgegeben, bis die max.  Anzahl erreicht ist. Verwende dazu die Methode GesamtkostenBerechnen.
8. KostenAusgeben (2)
   Letztlich wie BestellKostenAusgeben (1), nur das Abbruchkriterium der Schleife soll anders sein. Anfangen bei der Anzahl von 1 wird für jede weitere Anzahl eine Zeile ausgegeben, bis sich die Gesamtkosten  erhöhen. In der vorletzten Zeile befindet sich somit die optimale Anzahl.
   Benutze einmal eine while-do und einmal eine do-while Schleife.
9. Methode ueberschriftDrucken, die eine Überschriftenzeile erstellt und von den Methoden KostenAusgeben (1) – (3) ausgerufen wird. Diese Methode ist private.

Lösungshinweise:

1. Kopiere dazu die Lösung von optimaler Bestellmenge und ändere die Namen der Variablen. Lösche dann alle Methoden, die nicht benötigt werden.

Mögliche Bildschirmausgaben

ad 2 Bestandsinformationen:
Das Produkt Sneaker kostet in der Herstellung 50.0Euro.
Von diesem Produkt werden 12000.0 Stück gefertigt.
Die Rüstkosten betragen 150.0 Euro.
Der Lagerhaltungskostensatz beträgt 0.15%.

ad 5
Optimale Anzahl Lose berechnen
Die optimale Anzahl Lose pro Jahr beträgt 17.0.

ad 6
Optimale Losgröße berechnen
Die optimale Losgröße pro Jahr beträgt 706.0 Stück.

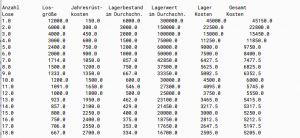
ad 7&8

Kosten ausgeben 2

 

Methoden zum Runden:

public static double rundenEuro(double betrag) {
//Runden – angepasst auf zwei Nachkommastellen
double d = Math.pow(10, 2);
return Math.round(betrag * d) / d;
}
public static double runden(double value, int nachkommastellen)
{//Runden -gefunden im Internet
double d = Math.pow(10, nachkommastellen);
return Math.round(value * d) / d;
}

Einfache Beispiele für eine Schleife – zum kopieren:
Zahl-do-while-2 & Zahl-do-while

Berechnung und optische Darstellung der optimalen Losgröße: Ab_Losgröße